Multigrafo
Es un grafo no orientado con
múltiples aristas entre pares de nodos. Un grafo es múltiple cuando usan
el mismo par de vértices. Un grafo que cuente con múltiples aristas entre dos
vértices se denomina multigrafo.
Otra definición similar es que un multígrafo es un grafo en el que hay pares de vértices unidos por más de una arista, es decir, que tiene aristas múltiples.
Un multigrafo G(V, E) consta de un
conjunto V de vertices, un conjunto E de aristas y una función f de E en {{u,
v}|u, v ∈ V, u 6= v}. Sedice que las aristas e1, e2 son aristas múltiples o
paralelas si f(e1) = f(e2).
Pseudografo
Un pseudografo es un grafo en el que hay aristas o lazos que tienen el mismo extremo.
Otra definición, es un conjunto de pares ordenados y etiquetados de elementos de V, es decir, un pseudografo dirigido es un grafo dirigido que acepta bucles en E.
Un pseudografo dirigido es un grafo G = (V,E) donde:


Adyacencia e incidencia
En un grafo, los vertices son adyacentes si están unidos mediante una arista.
Sea G= (V, A) un Grafo. Si (u, v) є A, decimos que el vértice v es adyacente al vértice u.
Grado de los Vértices Dos vértices u, v de un grafo G = (V, E) se dicen adyacentes si {u, v} ∈ E, asimismo dos aristas son adyacentes si tienen un mismo vértice como extremo; análogamente si e = {u, v} decimos que el lado e es incidente a los vértices u y v. El grado de un vértice es el número de lados incidentes a él. El grado de un vértice u se denota gr(u). Denotamos con ± (G) y ¢ (G) el mínimo y el máximo grado de los vértices de G respectivamente.
Aristas Adyacentes: dos aristas son adyacentes si convergen sobre el mismo vértice.
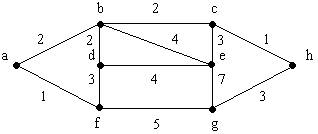
Grafo Ponderados
Es un Grafo Etiquetado (sus Aristas) con números Reales (A ≡ ℜ)
Llamamos grafos ponderados a los grafos en los que se asigna un número a cada una de las aristas. Este número representa un peso para el recorrido a través de la arista. Este peso podrá indicar, por ejemplo, la distancia, el costo monetario o el tiempo invertido, entre otros.
Definimos la longitud de un camino en un grafo ponderado como la suma delos pesos de las aristas de ese camino.
Definimos la longitud de un camino en un grafo ponderado como la suma delos pesos de las aristas de ese camino.
Ponderado o No ponderado: en los grafos ponderados, cada arco (o vértice) de G tiene asignado un valor numérico o peso. Los pesos para los arcos en redes de carreteras dependen de la aplicación específica, pero típicamente pueden ser la distancia, el tiempo de viaje o la máxima capacidad entre x e y.
La diferencia entre grafos ponderados y no ponderados es especialmente significativa cuando se trata de encontrar el camino más corto entre dos vértices. Para los grafos no ponderados, el camino más corto tiene que tener el menor número de arcos, y se puede encontrar mediante el algoritmo de recorrido en anchura.

Grafo Etiquetado
Es la asignación de etiquetas representado mediante enteros, a las aristas o vértices o ambos de un grafo.
El término grafo etiquetado generalmente se refiere a un grafo con vértices etiquetados con todas las etiquetas distintas.
Los grafos puede ser equivalentemente etiquetado mediante enteros consecutivos desde 1 hasta n, donde n es el número de vértices en el grafo.
Para muchas aplicaciones, a las aristas y los vértices le corresponden etiquetas que tienen un significado en el dominio asociado.
 |
| Grafo Elegante |
Grafo Nulo
Se dice que un grafo es nulo cuando los vértices que lo
componen no están conectados, esto es, que son vértices aislados. No
tiene vértices ni aristas, El grafo nulo es un caso particular
de grafo vacío, para los cuales sólo es requisito que el conjunto de
aristas sea vacío.
Grafo Vacio: Aquel que no tiene aristas.
Grafo Trivial
Aquel que tiene un vértice y ninguna arista.
Otra
definición, es un grafo con 0 aristas, y 0 ó 1 vértices.
Los grafo triviales son grafos completos:
a aquel que no posee vértices se le llama grafo nulo,
mientras que al que posee un vértice, se le conoce como grafo singleton.
Estos grafos son utilizados normalmente para comenzar una inducción matemática, o para buscar contraejemplos de
una proposición dada.
Grafo Simple
Aquel que no posee bucles o lazos. Un grafo simple es un grafo
o digrafo que no tiene bucles, y que no es un multigrafo.
- No tiene ciclos, esto es, no existe una arista en AG de la forma (v, v), donde v esta en VG.
- No hay más de un arista uniendo un par de nodos, esto es, no existe más de una arista en AG de la forma (v1, v2), para cualquier par de elementos v1 y v2 en VG.

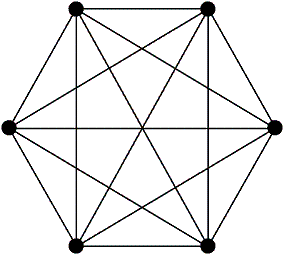
Grafo Completo
Es un grafo simple donde
cada par de vértices está conectado por una arista. Si existen
aristas uniendo todos los pares posibles de vértices. Es decir, todo
par de vértices (a, b) debe tener una arista e que los une.
Además es aquel con una arista entre cada par de vértices.
El conjunto de los grafos completos
es denominado usualmente, siendo el grafo completo
de n vértices.
Grafo Bipartido
Un
grafo G es bipartito si puede expresarse como G = {V1 U V2, A} (es
decir, sus vértices son la unión de dos grupos de vértices), bajo las
siguientes condiciones:
· V1
y V2 son disjuntos
y no vacíos.
· Cada
arista de A une un vértice de V1 con uno de V2.
· No
existen aristas uniendo dos elementos de V1; análogamente para V2.
Bajo estas condiciones, el grafo se considera bipartito, y puede
describirse informalmente como el grafo que une o relaciona dos conjuntos de
elementos diferentes, como aquellos resultantes de los ejercicios y puzzles en
los que debe unirse un elemento de la columna A con un elemento de la columna
B.

Grafo Bipartido Completo
Es aquel grafo bipartito en el que todos los vértices de lapartición 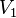 están conectados a todos los vértices de la partición
están conectados a todos los vértices de la partición 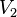 y viceversa.
y viceversa.
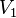 están conectados a todos los vértices de la partición
están conectados a todos los vértices de la partición 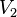 y viceversa.
y viceversa. |
| K3,1 (grafo estrella S3) |
Grafo Plano
Es un grafo que puede ser
dibujado en el plano sin que
ninguna aristase cruce (una definición más formal puede ser que este grafo
pueda ser "incrustado" en un plano).
Otra definición, Un grafo
G es planar si admite una representación en el plano de tal
forma que las aristas no se cortan, salvo en sus extremos. A dicha
representación se le denomina grafo plano. Se dice que un grafo es plano si puede dibujarse en el plano de manera
que ningún par de sus aristas se corte. A ese dibujo se le
llama representación plana del grafo
Un grafo es plano cuando se puede dibujar en dos dimensiones,
cuando ninguna arista cruza con otra.
 |
| Grafo Plano |
Grafo Rueda
Es un grafo con n vértices que
se forma conectando un único vértice a todos los vértices de un ciclo-(n-1).

Grafo Perfecto
Los grafos perfectos son aquellos
para los cuales esta cota inferior es exacta no sólo para el grafo en sí, sino
para todos los subgrafos inducidos. En los grafos en general, el número
cromático y el número de clique pueden ser distintos. Por ejemplo, un ciclo de
5 vértices requiere tres colores para obtener una coloración correcta, pero el
clique mayor es de tamaño dos.
Los grafos perfectos incluyen varias
familias de grafos importantes, y sirven para unificar resultados relacionados
con la coloración y los cliques en esas familias.